Encontrar cada triple pitagórico posible

Los triples pitagóricos son conjuntos de tres números enteros que satisfacen una relación muy específica: dos de esos enteros forman la base de un triángulo rectángulo, y el tercero es la hipotenusa. Hay muchos triples comunes, como $ (3, 4, 5) $, o $ (5, 12, 13) $, pero cuando aumentan las cifras, encontrar estos triples se convierte en una tarea difícil. ¿Es posible generar estos triples por un proceso matemático? Para resolver esta cuestión, empezamos por examinar qué hace única la relación entre números en un triple pitagórico.

Último Teorema de Fermat #

Para resolver cualquier tipo de problema matemático, a menudo es útil relacionarlo con problemas más generales que pueden proporcionar un poco de contexto para guiar el proceso de encontrar una solución. El problema de encontrar todos los triples pitagóricos posibles es un buen ejemplo de esto. Fundamentalmente estamos intentando despejar $ A $, $ B $ y $ C $ tal que:

$$ A^2 + B^2 = C^2 \space \textnormal{donde} \space A, B, C \in \Z $$

De hecho, hay infinidad de $ A $, $ B $ y $ C $ tal que esta ecuación es cierta. Sin embargo, una peculiaridad más sutil es que el teorema pitagórico es un caso muy especial de un problema mucho mayor donde esta propiedad no existe. Si consideramos el mismo problema de despejar $ A $, $ B $ y $ C $, pero simplemente cambiamos el exponente y pedimos soluciones enteras:

$$ A^n + B^n = C^n \space \textnormal{donde} \space A, B, C, n \in \Z \space \cap \space n > 2 $$

no hay soluciones infinitas, sino cero soluciones no triviales. Es decir que hay cero soluciones donde todos $ A, B, C \neq 0 $. Este es el Último Teorema de Fermat, que declara que la ecuación $ A^n + B^n = C^n $ no tiene soluciones enteras si $ n > 2 $. Esta simple declaración es engañosamente difícil de probar; tardó más de tres siglos hasta que una prueba formal se presentó tras la propuesta inicial de Fermat en 1637 dC.

Aunque probar matemáticamente que la declaración es cierta es bastante difícil, es muy sencillo ver sus consecuencias cuando estudiamos este problema de una perspectiva visual. Para hacer eso, necesitaremos graficar esta ecuación como un tipo de curva en el plano cartesiano. Aunque podríamos continuar a graficar esta ecuación en tres dimensiones, podemos hacer una sustitución ingeniosa para graficar la curva en dos dimensiones. Si dividimos ambos lados por $ C^n $, obtenemos:

$$ \left( \frac{A}{C} \right)^n + \left( \frac{B}{C} \right)^n = 1 $$

Ahora, nos damos cuenta de que tanto $ \frac{A}{C} $ como $ \frac{B}{C} $ son números racionales, como los numeradores y los denominadores de las dos fracciones son números enteros. Esto quiere decir que podemos hacer una sustitución:

$$ (x, y) = \left( \frac{A}{C}, \frac{B}{C} \right) $$

Ahora estamos buscando soluciones a la ecuación:

$$ x^n + y^n = 1 \space \textnormal{donde} \space x, y \in \mathbb{Q} $$

Por ahora, solamente consideramos los casos donde $ n > 2 $. Graficar la ecuación para varios valores de $ n $ pone de manifiesto dos familias de curvas: una familia donde $ n $ es par y otro donde $ n $ es impar.

Cuando aumentamos el valor de $ n $, las curvas se parecen a una de las dos familias de curvas mostradas arriba, dependiendo de si $ n $ es par o impar. Los valores más grandes de $ n $ resultan en esquinas más cerradas, causando la curva a parecerse más a un cuadrado. Ahora, volvemos al caso donde $ n = 2 $ y preguntamos ¿qué hace este caso distinto a todos los demás?

$$ x^2 + y^2 = 1 $$

De hecho, la curva en este caso no es una curva al azar sino más bien uno de los objetos más comunes en todas las matemáticas: el círculo unitario. Combinando esto con nuestro conocimiento que hay infinidad de triples pitagóricos, podemos deducir que debe haber infinidad de puntos en el círculo unitario donde $ x, y \in \mathbb{Q} $. Llamamos tal punto con coordenadas racionales un punto racional en el círculo unitario.

Haciendo este proceso en orden inverso, dado un punto racional en el círculo unitario $ (x, y) $, podemos reescribir $ x $ e $ y $ como fracciones $ \frac{a}{b} $ y $ \frac{c}{d} $, respectivamente. Entonces tenemos:

$$ \left( \frac{a}{b} \right)^2 + \left( \frac{c}{d} \right)^2 = 1 $$

Eliminando los denominadores da:

$$ (ad)^2 + (bc)^2 = (bd)^2 $$

¡Este es un triple pitagórico! Simplemente definimos:

$$ (A, B, C) = (ad, bc, bd) $$

Por lo tanto, hay una relación directa entre puntos racionales en el círculo unitario y los triples pitagóricos. Encontrar uno nos da el otro. En otras palabras, nuestro problema ya no es «encontrar todos los triples pitagóricos» sino «encontrar todos los puntos racionales en el círculo unitario».

Puntos racionales en una cónica #

Hasta ahora, hemos reducido el problema de encontrar todos los triples pitagóricos posibles a encontrar todos los puntos racionales en el círculo unitario. Si encontramos un punto racional en el círculo unitario, entonces sabemos que se corresponde a un único triple pitagórico. Para ser justo, esto probablemente no es una gran simplificación: hemos reducido un problema difícil a otro que en un principio parece aún más difícil: ¿cómo se puede encontrar puntos racionales en una curva? Y, por si fuera poco, ¿cómo se encuentra cada punto racional? Al igual que la sección anterior, vamos a generalizar un poco con la esperanza de referir este problema a otros y alternadamente encontrar un patrón que ayude a reducir este problema a uno que se pueda resolver más fácilmente.

En la última sección, acabamos preguntando cómo encontrar cada punto racional en el círculo unitario. Este capítulo, vamos a hacer un poco más; preguntamos: ¿cómo se encuentra cada punto racional en una cónica de forma más general? Primero, tenemos que definir lo que entendemos por una cónica «de forma más general». Normalmente pensamos en las cónicas como el resultado de secciones transversales de un cono en diferentes ángulos. De estas secciones transversales obtenemos los cuatro cónicos estándar: círculos, elipses, parábolas e hipérbolas. Cuando se grafican estas figuras en el plano cartesiano y se tiene en cuenta la rotación, todos tienen una ecuación de la forma:

$$ A x^2 + B y^2 + C xy + D x + E y + F = 0 $$

dados algunos coeficientes $ A, B, C, D, E, F $ donde $ AB \neq 0 $. En otras palabras, las cónicas solamente son curvas algebraicas (a menudo llamadas «variedades algebraicas») de grado $ 2 $. Aquí está el gráfico de una cónica arbitraria $ \mathcal{C} $: $ x^2 + y^2 + xy + x + y - 1 = 0 $:

Con respecto a nuestro problema, asumiremos que $ \mathcal{C} $ contiene algún punto racional $ \mathcal{O} $ que conozcamos. En este caso, $ \mathcal{O} $ es el punto $(-1, 1) $. Lo que vamos a hacer es crear una función generadora para cada otro punto racional en $ \mathcal{C} $ simplemente por conocer $ \mathcal{O} $.

Una interesante observación que podemos hacer es que si sabemos el valor de una variable, digamos $ y $, en materia de una función lineal $ \ell $ de la otra, podemos sustituirla en la ecuación de la cónica para obtener una ecuación cuadrática de solo una variable. Las soluciones de la ecuación cuadrática que resulta del paso anterior nos da las intersecciones entre la cónica $ \mathcal{C} $ y la función lineal $ \ell $. Una propiedad conveniente de las ecuaciones cuadráticas es que el término constante $ c $ de la ecuación $ a x^2 + b x + c = 0 $ siempre es un múltiplo del producto de las dos soluciones. Esto resulta del hecho de que, según el Teorema Fundamental del Álgebra, cualquiera ecuación cuadrática puede reescribirse como:

$$ a x^2 + b x + c = a(x - r)(x - s) $$

dadas algunas soluciones $ r, s $. Multiplicando los factores da:

$$ a x^2 + b x + c = a x^2 - a(r + s) x + ars $$

Igualar los términos constantes al uno al otro da:

$$ c = ars $$

Asumiremos que tanto la cónica como la expresión lineal de $ y $ en materia de $ x $ tienen coeficientes exclusivamente racionales para que esta ecuación cuadrática tenga coeficientes racionales también. Si sabemos que una solución $ s $ es racional, entonces la otra solución $ r $ debe ser racional también como:

$$ r = \frac{c}{as} \space \textnormal{donde} \space c, a, s \in \mathbb{Q} $$

Para resumir nuestro trabajo hasta ahora y su relevancia a resolver este problema, sabemos que si podemos expresar $ y $ como una función lineal de $ x $ con coeficientes racionales, entonces podemos sustituir $ y $ en la ecuación para obtener una ecuación cuadrática de $ x $. Y, si esa ecuación cuadrática tiene de casualidad una solución racional $ x = s $, entonces la segunda solución $ x = r $ también debe ser racional. Ahora, esto probablemente parece un poco complicado e inútil, pero el primer paso debería darnos una pista de lo que necesitamos hacer: escribir $ y $ como una función lineal de $ x $.

Una función lineal tiene la forma $ y = a x + b $ donde asumiremos que $ a $ y $ b $ son coeficientes racionales para que la ecuación cuadrática que resulta contenga coeficientes exclusivamente racionales también. Nos referiremos a tal línea como una «línea racional» y nos referiremos a una cónica con coeficientes racionales como una «cónica racional». La clave para nuestra solución radica en escoger una línea tal que cuando este valor de $ y $ se sustituye en $ \mathcal{C} $, obtenemos una ecuación cuadrática de $ x $ con por lo menos una solución racional, y implicando así la existencia de otra solución racional, dándonos otro punto en la cónica con una coordenada racional para $ x $.

Como apuntado antes, lo que esencialmente estamos haciendo cuando sustituimos una ecuación lineal $ \ell $ por $ y $ en $ \mathcal{C} $ es encontrar la intersección entre esta línea y la cónica. En otras palabras, el problema de hallar una función lineal tal que su sustitución en $ \mathcal{C} $ dé una ecuación cuadrática de $ x $ con al menos una solución racional equivale a hallar una línea que cruce $ \mathcal{C} $ en algún punto con una coordenada racional para $ x $.

¡Pero tenemos un punto así! Antes, definimos $ \mathcal{O} $ como un punto racional en $ \mathcal{C} $, que quiere decir que sus dos coordenadas son racionales. Si trazamos una línea a través de $ \mathcal{O} $ que cruce $ \mathcal{C} $ en otro punto $ P $, tenemos una segunda solución para $ x $ en la ecuación cuadrática. Pero como $ \mathcal{O} $ es un punto racional, la ecuación cuadrática ya tiene una solución racional, y por lo tanto su segunda solución debería ser racional también, que quiere decir que la intersección $ P $ tiene una coordenada racional para $ x $. Pero, si nuestra línea es racional también, entonces podemos hallar la coordenada correspondiente para $ y $ como $ a x + b $, que quiere decir que un valor racional para $ x $ implica un valor racional para $ y $ para cada punto en la línea. Por lo tanto, nuestro segundo punto de intersección tiene una coordenada racional para $ x $ y una coordenada racional para $ y $, haciéndolo un punto racional en $ \mathcal{C} $.

Aquí está un ejemplo:

La línea racional $ y = -2x - 1 $ a través de $ \mathcal{O} $ cruza la elipse otra vez, produciendo un segundo punto racional $ \left( \frac{1}{3}, -\frac{5}{3} \right) $. Visualmente, es fácil ver que si queremos encontrar todos los puntos racionales en $ \mathcal{C} $, necesitamos considerar cada línea racional a través de $ \mathcal{O} $ para que recorramos el plano entero. Matemáticamente, se sabe que, dados dos puntos racionales, la recta entre ellos debe tener una pendiente racional, porque su pendiente puede reescribirse como el cociente de sus diferencias de $ x $ e $ y $, que alternadamente son racionales. Si trazamos una recta para cada posible pendiente racional, inevitablemente encontraremos todos los puntos racionales.

Ahora el problema es simplemente cómo parametrizar la cónica $ \mathcal{C} $ para que tengamos en cuenta todos los puntos racionales y solamente los puntos racionales. Llamamos a tal parametrización una «parametrización racional» de la cónica $ \mathcal{C} $. Parametrizaciones racionales parametrizan una curva $ \mathcal{C} $ en función de una variable $ t $ tal que cada $ t $ racional se corresponde a una pareja de coordenadas racionales $ (x, y) $.

En este punto, ciertamente podríamos parametrizar $ \mathcal{C} $ en materia de la pendiente de la recta. Sin embargo, una manera más agradable geométricamente de pensar en esto implica trazar una segunda línea racional. Tener en cuenta todas las pendientes quiere decir que necesitamos escoger un segundo punto que constantemente se mueve en algún lugar del plano cartesiano para cambiar la pendiente de nuestra línea continuamente. Ya sabemos que la pendiente entre dos puntos racionales es racional, así que solamente necesitamos encontrar un conjunto de puntos racionales en el plano que satisfagan esta condición de tener una pendiente que cambia continuamente.

Una línea racional ofrece la respuesta perfecta. Pasando por cada punto en una línea racional, cambiamos la pendiente de la línea que cruza la cónica. Eso es porque dos líneas con pendientes distintas cruzan en un solo punto. En el ejemplo, una de las líneas (la línea de la que estamos escogiendo el conjunto de puntos) nunca cambia su pendiente. Por consiguiente, para que el punto de intersección cambie, la línea que cruza la cónica debe cambiar su pendiente. Recorrer todos los puntos posibles en una línea racional genera líneas de intersección con todas las posibles pendientes (con una sola excepción, que veremos más tarde). Un diagrama geométrico aclarará este concepto intuitivamente.

El algoritmo es el siguiente:

1. Escoger un número racional $ t $ para parametrizar $ \mathcal{C} $
2. Evaluar $ f(t) $, dada alguna función racional lineal $ f(x) = c x + d $ para generar algún punto racional $ Q $ en $ f $
3. Trazar una línea $ \ell $ a través de los puntos $ \mathcal{O} $ y $ Q $, donde $ \mathcal{O} $ es un punto racional en $ \mathcal{C} $
4. Despejar la intersección $ \ell \cap \mathcal{C} $, que da el deseado punto racional $ P $ en $ \mathcal{C} $

$ f(t) $ se grafica en verde; $ t $ determina el punto $ Q $ (de púrpura) en $ f $; la línea que conecta $ Q $ y $ \mathcal{O} $ es azul y cruza la cónica en el punto $ P $

De hecho, estamos «proyectando» la cónica $ \mathcal{C} $ en $ f(t) $, que alternadamente forma un mapeo único entre puntos en $ \mathcal{C} $ y puntos en $ f(t) $, que aprovechamos para parametrizar racionalmente cualquier cónica. Algo que debería notarse antes de pasar a los círculos es que este método no encuentra cada punto racional; específicamente, falta exactamente un punto. Esto ocurre en el punto donde la tangente en la cónica $ \mathcal{C} $ es exactamente paralela a la línea $ f(t) $ de la que estamos escogiendo $ Q $. Esto, alternadamente, significa que las dos líneas nunca cruzan y, por lo tanto, no hay un punto $ Q $ en $ f(t) $ que se corresponda a este punto en la cónica. Presentamos esto más como un tecnicismo, que como un problema grave, ya que no plantea más problemas en nuestra búsqueda de todos los triples pitagóricos. Si le interesa si es posible incluir este punto misterioso en nuestra parametrización, sepa que sí es posible cuando se usa el plano proyectivo, donde declaramos que este punto se corresponde a $ t = \infty $, aunque eso es un matiz que ignoraremos.

La sustitución de Weierstrass #

¡Genial! 🎉 El trabajo duro está (principalmente) hecho. Nosotros necesitábamos parametrizar racionalmente el círculo unitario, pero en vez de eso, desarrollamos una parametrización racional para cada cónica. Ahora lo único que tenemos que hacer es inventar una manera eficiente de ejercer lo que hemos aprendido desde la sección anterior al círculo unitario.

Para parametrizar racionalmente una cónica, necesitamos dos cosas: un punto racional $ \mathcal{O} $ y una línea racional en la que se puede proyectar la cónica. En el caso del círculo unitario, tenemos cuatro «obvios» puntos racionales: $ (\pm 1, 0), (0, \pm 1) $. Para razones que se aclararán más tarde, escojamos el punto $ (-1, 0) $ para ser $ \mathcal{O} $. Para la línea racional de proyección, tenemos infinidad de opciones. Sin embargo, aunque nuestro ejemplo anterior mostraba la línea racional fuera de la cónica, no es necesario que la línea de proyección no cruce la cónica misma. A veces, las mejores opciones son las más obvias; en nuestro caso, esas son los ejes $ x $ e $ y $ ellos mismos. Vemos inmediatamente que el eje $ x $ no vale, ya que sin importar qué punto escojamos, la línea desde $ (-1, 0) $ tendrá una pendiente de $ 0 $, y por lo tanto solamente cruzará el círculo en el punto $ (1, 0) $. El eje $ y $ queda como la siguiente opción más fácil.

Pasando al segundo paso en nuestro algoritmo, necesitamos establecer un mapeo entre un número racional $ t $ y un punto racional por el eje $ y $. Podemos hacer eso fácilmente parametrizando el eje $ y $ como $ (0, t) $. Esto nos da el punto $ Q $ para el tercer paso.

Ahora trazamos la línea $ \ell $ a través de $ \mathcal{O} $ y $ Q $, que viene de la ecuación $ y = t(x + 1) $. El resultado del algoritmo, la intersección $ \ell \cap \mathcal{C} $, nos da el deseado punto racional $ P $. La sustitución de la definición de $ y $ desde $ \ell $ en la definición del círculo unitario da:

$$ x^2 + t^2(x + 1)^2 = 1 $$

Una reorganización produce:

$$ t^2(1 + x)^2 = 1 - x^2 $$ $$ t^2(1 + x)\cancel{(1 + x)} = \cancel{(1 + x)}(1 - x) $$ $$ t^2(1 + x) = 1 - x $$

En este punto podemos despejar $ x $ en materia de $ t $ para obtener:

$$ x = \frac{1 - t^2}{1 + t^2} $$

La sustitución de esto en la definición de $ \ell $ produce un valor para $ y $ también:

$$ y = t \left( \frac{1 - t^2}{1 + t^2} + 1 \right) = t \left( \frac{2}{1 + t^2} \right) = \frac{2t}{1 + t^2} $$

La combinación de estas dos igualdades produce la parametrización racional del círculo unitario:

$$ (x, y) = \left( \frac{1 - t^2}{1 + t^2}, \frac{2t}{1 + t^2} \right) $$

Vemos inmediatamente que, dado un valor de $ t \in \mathbb{Q} $, debemos obtener un punto racional correspondiente en el círculo unitario, ya que generar este punto consiste en solo la multiplicación, división, adición y sustracción, que, cuando se aplican a números racionales, siempre producen un número racional. Tenga en cuenta que esto no sería el caso si hubiéramos usado la familiar ecuación paramétrica del círculo unitario $ (\cos \theta, \sin \theta) $; aún si fuera verdad que $ \theta \in \mathbb{Q} $, no podemos garantizar que el resultado de tampoco $ \cos \theta $ ni $ \sin \theta $ producirá un resultado racional (trate de expresar el punto $ (\cos 1, \sin 1) $ en materia de coordenadas racionales).

Aunque nuestro resultado es obviamente importante algebraicamente, también es importante examinarlo de una perspectiva geométrica.

Los puntos en el círculo unitario se proyectan en el eje $ y $, donde los puntos en los primeros y cuartos cuadrantes se convierten en puntos dentro del círculo unitario (la región donde $ -1 \leq t \leq 1 $) y los puntos en los segundos y terceros cuadrantes se convierten en puntos fuera del círculo unitario (donde $ |t| > 1 $).

Lo que vamos a hacer ahora no se relaciona directamente con el problema de encontrar todos los triples pitagóricos posibles, así que puede saltar a la siguiente sección si quiere. Sin embargo, el proceso que vamos a explorar es tan importante que es casi imposible saltar ahora que hemos descubierto la parametrización racional del círculo unitario.

Antes, se insinuó que, de los cuatro puntos racionales que podríamos haber elegido para ser $ \mathcal{O} $, había una razón por la que $ (-1, 0) $ se escogió en particular. Esa razón, como se puede ver ahora, es que $ t $ se convierte en la pendiente de la línea $ \ell $, que simplifica las matemáticas que vamos a hacer. Vamos a explorar la respuesta a una siguiente pregunta muy obvia, que es: ¿cómo relacionamos la parametrización racional del círculo a su parametrización tradicional como $ (\cos \theta, \sin \theta) $? Más concretamente, estamos preguntando:

Dado un punto de la forma $ (\cos \theta, \sin \theta) $ para algún ángulo $ \theta $, ¿cuál es el valor correspondiente de $ t $ que genera ese punto en la parametrización racional?

De hecho, vamos a olvidarnos de la condición $ t \in \mathbb{Q} $ que impusimos para asegurar que la parametrización producía solamente puntos racionales y, en vez de eso, vamos a extender el dominio de $ t $ a $ t \in \R $. Tomando una perspectiva más geométrica, estamos intentando a despejar el valor $ t $ mostrado en el diagrama de abajo:

Cuando la distancia del punto racional $ (-1, 0) $ hasta el origen es solamente 1, podemos usar la tangente de $ \varphi $ para despejar $ t $. Ahora todo lo que tenemos que hacer es expresar $ \varphi $ en materia de $ \theta $. Si conoce bien la geometría, notará que $ \varphi $ es un ángulo inscrito y, por lo tanto, es la mitad del ángulo $ \theta $. Una prueba corta de este teorema se muestra abajo (en el caso donde una cuerda es el diámetro, como en el diagrama):

Por lo tanto:

$$ t = \tan \varphi = \tan \frac{\theta}{2} $$

Ahora podemos equiparar las dos parametrizaciones:

$$ (\cos \theta, \sin \theta) = \left( \frac{1 - t^2}{1 + t^2}, \frac{2t}{1 + t^2} \right) \space \textnormal{donde} \space t = \tan \frac{\theta}{2} $$

Bueno, ¿y qué? Ya sabíamos que las dos parametrizaciones describían el mismo objeto, así que ¿por qué deberíamos equipararlas? De hecho, ¿por qué no hicimos el contrario preguntando expresar nuestra parametrización en materia de la parametrización común $ (\cos \theta, \sin \theta) $ mediante despejar $ \theta $ en materia de $ t $? Resulta que eso es lo que vamos a hacer muy pronto, pero de una manera un poco diferente. Sin embargo, la razón principal por la que esta ecuación es tan importante es porque nos da una manera alternativa de expresar las funciones trigonométricas $ \cos x $ y $ \sin x $:

$$ \textnormal{Equiparar: } t = \tan x/2 $$ $$ \sin x = \frac{2t}{1 + t^2} $$ $$ \cos x = \frac{1 - t^2}{1 + t^2} $$

En otras palabras, no solo hemos parametrizado el círculo unitario en materia de $ t $, sino también hemos hecho lo mismo a las funciones trigonométricas de $ \sin $ y $ \cos $. Ahora podemos expresar las dos funciones trigonométricas más fundamentales en materia de un solo parámetro $ t $, que alternadamente nos permite expresar todas las seis funciones trigonométricas comunes en materia de $ t $ también. Esta sustitución se conoce como la «sustitución de Weierstrass», de ahí el nombre de esta sección.

Para entender lo que esto significa y la razón por la que es tan importante, considere la identidad trigonométrica bastante compleja:

$$ \frac{\cos^{4} x -\sin^{4} x}{\cos^{2}x} = 1-\tan^{2}x $$

Su primer instinto es probablemente tratar de descomponer el término problemático $ \sin x $ en factores y entonces esperar que todo simplifica para producir un término $ \tan^{2}x $ de alguna manera. Pero, ¿qué tal si todas las tres funciones trigonométricas pudieran expresarse en materia de una sola variable $ t $? Entonces, el problema es simplemente álgebra: simplificar las funciones racionales de $ t $ en ambos lados y mostrar que son equivalentes. Si expresamos todo en materia de $ t $ usando la sustitución de Weierstrass y si entonces escribimos ambos lados como funciones racionales, produciría algo así:

$$ \frac{\left(1-t^{2}\right)^{4}-\left(2t\right)^{4}}{\left(1-t^{2}\right)^{2}\left(1+t^{2}\right)^{2}} = 1-\frac{\left(2t\right)^{2}}{\left(1-t^{2}\right)^{2}} $$

La combinación del lado derecho en una fracción da:

$$ \frac{\left(1-t^{2}\right)^{2}-\left(2t\right)^{2}}{\left(1-t^{2}\right)^{2}} $$

La eliminación de los denominadores en el lado derecho da:

$$ \frac{\left(1-t^{2}\right)^{4}-\left(2t\right)^{4}}{\left(1+t^{2}\right)^{2}} = \left(1-t^{2}\right)^{2}-\left(2t\right)^{2} $$

Al eliminar los denominadores una vez más, ahora en el lado izquierdo, la ecuación es:

$$ \left(1-t^{2}\right)^{4}-\left(2t\right)^{4} = \left(1+t^{2}\right)^{2}\left(\left(1-t^{2}\right)^{2}-\left(2t\right)^{2}\ \right) $$

En este momento, simplemente podemos ampliar todos los binomios para obtener:

$$ 1-4t^{2}-10t^{4}-4t^{6}+t^{8} = \left(1+2t^{2}+t^{4}\right)\left(1-6t^{2}+t^{4}\right) $$

Realizar la división larga prueba que sí esta es la factorización correcta del polinomio a la izquierda, implicando que la identidad debería ser cierta. Aunque este proceso implica, por supuesto, significativamente más álgebra que el enfoque tradicional de probar estas identidades, es una herramienta inmensamente útil para resolverlas porque provee una manera de convertir problemas de trigonometría en problemas de álgebra, posibilitando un enfoque sistemático para probar que una dada identidad es verdadera o falsa.

De hecho, estas identidades son herramientas sumamente útiles en el cálculo también. Digamos que queremos evaluar la integral indefinida:

$$ \int \csc x \space dx $$

Podríamos muy bien expresar esto en materia de $ \sin x $ para obtener:

$$ \int \frac{dx}{\sin x} $$

pero esto no vale—hasta que usemos la sustitución de Weierstrass. Para hacerlo, sin embargo, necesitaremos expresar $ x $ en materia de $ t $ para sustituir el término $ dx $ por una expresión de $ t $. Recuerde que por la definición de $ t $, sabemos:

$$ t = \tan x/2 \Rightarrow x = 2 \arctan t $$

Esta es esencialmente la sustitución de Weierstrass a la inversa: nos da una manera de escribir la parametrización racional del círculo unitario en materia de la parametrización tradicional de $ (\cos \theta, \sin \theta) $. El uso de ese hecho para reescribir la integral da:

$$ \int \frac{1 + t^2}{2t} \space d(2 \arctan t) = \int \frac{1 + t^2}{2t} \space \frac{d}{dt}(2 \arctan t) \space dt $$

La multiplicación por la derivada de $ 2 \arctan t $ produce una expresión racional en materia de $ t $ de que podemos calcular la integral:

$$ \int \frac{\cancel{1 + t^2}}{2t} \cdot \frac{2}{\cancel{1+t^{2}}} \space dt = $$ $$ \int \frac{\cancel{2}}{\cancel{2}t} \space dt = \int \frac{dt}{t} $$

¡Ajá! Hemos reducido el problema a una integral fundamental. Ahora podemos calcular la integral y sustituir $ t = \tan x/2 $ para obtener:

$$ \int \frac{dt}{t} = \ln |t| = \ln |\tan x/2| $$

¡Viola! La sustitución de Weierstrass transformó la integral en una forma común de que podríamos calcular la respuesta y entonces sustituir $ t = \tan x/2 $ para obtener una solución.

Los primitivos #

Por fin volvemos al problema de encontrar todos los posibles triples pitagóricos. Hemos discutido las curvas de Fermat y la peculiaridad del teorema pitagórico, la parametrización racional de las cónicas, y más recientemente la sustitución de Weierstrass. Finalmente podemos resolver el problema de encontrar todos los triples pitagóricos.

Empezamos notando la manera más obvia de generar un nuevo triple pitagórico: si conocemos un triple $ (A, B, C) $, entonces simplemente podemos generar un nuevo triple $ (tA, tB, tC) $, dado algún número entero $ t $. Sin embargo, estos triples no son tan útiles y en última instancia resultan del triple común $ (A, B, C) $. En otras palabras, si podemos encontrar todos los triples $ (A, B, C) $ donde $ A, B, C $ no tienen ningún factor común (vale decir $ \gcd(A, B, C) = 1 $), entonces podemos generar todos los otros triples, simplemente multiplicando por un número entero $ t $. Por ahora nos centraremos en los triples comunes, que llamaremos los triples «primitivos».

La última restricción viene de una propiedad interesante que todos los triples primitivos comparten: siempre contienen un término par y un término impar de $ A $ y $ B $. Para probar esto, tenemos que aprovechar un poco de la teoría de números elemental. El primer caso es que tanto $ A $ como $ B $ son pares. Queremos forzar una contradicción que requeriría que $ A $, $ B $ y $ C $ tengan un factor común. Si consideramos este escenario en módulo $ 2 $, obtenemos:

$$ A^2 + B^2 \equiv 0^2 + 0^2 = 0 \equiv C^2 \mod 2 $$ $$ A \equiv B \equiv C \equiv 0 \mod 2 $$

Esa última parte deriva del hecho de que si $ 2 \mid C^2 $, como $ 2 $ es primo, también debe ser cierto que $ 2 \mid C $. Entonces hemos probado que todos $ A $, $ B $ y $ C $ deberían ser par, que significa que el triple no es primitivo (todos los términos se pueden dividir por $ 2 $). Por eso podemos descartar esa posibilidad. El siguiente caso requiere probar que es imposible que $ A $ y $ B $ sean impares a la vez. Consideramos la situación en módulo $ 4 $:

$$ A^2 + B^2 \equiv \set{ 1, 3 }^2 + \set{ 1, 3 }^2 \equiv 1 + 1 = 2 \equiv C^2 \mod 4 $$

* Se usa la notación para un conjunto $ \set{} $ aquí para indicar todas las posibilidades de congruencia

La ecuación anterior prueba que $ C^2 $ debería ser divisible por 2, pero no por 4. Pero si $ C^2 $ es divisible entre 2, ya que 2 es primo, también debe dividir $ C $ sí mismo. Pero si 2 divide $ C $, entonces $ 2 \times 2 $ divide $ C^2 $, que, de ese modo, implica que $ 4 $ divide $ C^2 $, la contradicción que buscábamos. Por lo tanto, cada triple pitagórico primitivo debe tener un $ A $ o $ B $ par y el otro impar. Para el resto de esta sección, asumiremos que $ A $ es impar y $ B $ es par.

Como se señaló en la primera sección, cualquier triple pitagórico $ (A, B, C) $ puede convertirse en un punto en el círculo unitario como el punto $ (x, y) = (A/C, B/C) $ (triples primitivos y sus múltiplos representan el mismo punto). Esto significa que cada posible triple pitagórico primitivo corresponde a un punto único racional en el círculo unitario; si encontramos todos los puntos racionales en el círculo unitario, hemos encontrado todos los triples pitagóricos. ¡Pero sabemos hacerlo!

En ese punto, por supuesto podríamos usar la parametrización racional del círculo unitario que obtuvimos anteriormente para encontrar todos los triples pitagóricos. Sin embargo, vamos a imponer la restricción de generar exclusivamente primitivos triples pitagóricos. También tenga en cuenta que si simplemente usáramos la parametrización racional tal cual, terminaríamos con muchos triples no primitivos cuando $ |t| > 1 $ y muchos triples con fracciones cuando $ |t| < 1 $ (que realmente no son triples porque $ A, B, C \notin \Z $).

La estrategia clave es definir $ t = p/q $, dados números enteros $ p $ y $ q $. La expresión de $ t $ de forma «racional» nos permite expresar el resultado de una forma racional similar, de la cual podemos generar un triple pitagórico no fraccionario. La sustitución $ t = p/q $ en la parametrización racional del círculo unitario da:

$$ \left(\frac{q^{2}-p^{2}}{q^{2}+p^{2}},\frac{2pq}{q^{2}+p^{2}}\right) $$

Inmediatamente podemos ver que, dado $ p < q $, obtenemos una serie de tres números enteros que es un triple pitagórico: $ (q^2-p^2, 2pq, q^2+p^2) $. Tenga en cuenta que $ p < q $ realmente no es una restricción, ya que solo asegura que todos los triples que se generan tengan valores positivos para $ A, B, C $.

Ahora todo lo que queda es probar rigurosamente que el triple pitagórico anterior siempre es primitivo, sin importar los valores de $ p $ y $ q $. Sin embargo, como estamos expresando $ t $ en forma más simple para evitar duplicados, $ p $ y $ q $ necesitan ser relativamente primos, que es la primera restricción que impondremos antes de llevar a cabo la prueba. La última restricción es que, para que $ A $ sea impar como asumimos, $ 2 \nmid (q^2 - p^2) $, que fuerza que $ p $ o $ q $ sea par y el otro sea impar. Combinando todas las restricciones produce:

1. Dominio: $ p, q \in \mathbb{Z}^{+} $
2. Positividad: $ p < q $
3. Primalidad relativa: $ \gcd(p, q) = 1 $
4. Números pares e impares: $ (2 \mid p \cap 2 \nmid q) \cup (2 \nmid p \cap 2 \mid q) $

Ahora continuamos probando que el triple $ (q^2-p^2, 2pq, q^2+p^2) $ sí es primitivo. Empezamos sin asumir que el triple generado sea primitivo. En vez de eso, definamos el triple como un múltiplo constante $ \lambda $ de un triple primitivo $ (A, B, C) $ tal que:

$$ \lambda A = q^2 - p^2 $$ $$ \lambda B = 2pq $$ $$ \lambda C = q^2 + p^2 $$

Si podemos demostrar que $ \lambda = 1 $, entonces hemos probado con éxito que el triple es primitivo, ya que significaría que nuestro triple primitivo $ (A, B, C) $ es igual que los valores deseados exactamente. Como $ A, B, C \in \mathbb{Z} $, $ \lambda $ debe dividir los términos en el lado derecho de estas expresiones. De esto podemos obtener:

$$ \lambda \mid q^2 - p^2 $$ $$ \lambda \mid 2pq $$ $$ \lambda \mid q^2 + p^2 $$

La primera y tercera expresión es específicamente interesante; como $ \lambda $ divide las dos, también debe dividir su suma y diferencia. Esto produce:

$$ \lambda \mid 2q^2 $$ $$ \lambda \mid 2p^2 $$

Si $ \lambda $ dividiera $ p^2 $ y $ q^2 $, entonces al menos uno de sus factores primos se compartiría por $ p $ y $ q $; pero esto contradice el tercer supuesto que $ p $ y $ q $ necesitan ser relativamente primos. Por lo tanto, $ \lambda $ debe dividir $ 2 $. Alternadamente, esto significa que solamente quedan dos opciones para $ \lambda $, que reduce enormemente el conjunto de todos los valores posibles a los factores de dos: $ 1, 2 $.

Ahora asumimos que $ \lambda = 2 $ y buscamos una contradicción. Sabemos que $ A $ es impar, así que $ A \equiv 1 \space \mathrm{mod}\ 2 $. Esto produce:

$$ \lambda A = 2A \equiv 2 \mod 4 $$

¡Ajá! ¡Ya lo hemos visto antes! En la prueba que $ A $ y $ B $ no podían ser impares, demostramos que es imposible que el cuadrado de un número entero sea congruente con $ 2 \space \mathrm{mod}\ 4 $. Tenemos una definición similar para $ \lambda A $ que podemos aprovechar:

$$ \lambda A = q^2 - p^2 \equiv 2 \mod 4 $$

En lugar de probar que el cuadrado de un número entero no puede ser congruente con $ 2 \space \mathrm{mod}\ 4 $, necesitamos probar que la diferencia de los cuadrados de dos números enteros no puede ser congruente con $ 2 \space \mathrm{mod}\ 4 $. El proceso es casi idéntico*:

$$ q^2 - p^2 \equiv \set{0,…,3}^2 - \set{0,…,3}^2 \equiv \set{0,1} - \set{0,1} = \set{0,-1,1} \mod 4 $$

* También podríamos haber aplicado la restricción que solo uno de $ p $ y $ q $ es par, pero esto no es necesario para terminar la prueba

Cuando simplificamos el conjunto para que contenga exclusivamente los números enteros positivos, la contradicción se hace patente inmediatamente:

$$ 2 \notin \set{0,1,3} $$

De esto podemos concluir que la diferencia de los cuadrados de dos números enteros no puede ser congruente con $ 2 \space \mathrm{mod}\ 4 $, y alternadamente $ \lambda $ no puede valer $ 2 $, que significa que $ \lambda = 1 $, como deseamos.

✨ ¡Hemos probado que el triple $ (q^2-p^2, 2pq, q^2+p^2) $ es primitivo!

En el plano cartesiano #

Por fin tenemos un algoritmo generativo para hallar cada posible triple pitagórico primitivo, que alternadamente nos da cada triple pitagórico multiplicando el triple por una constante entera. El algoritmo básicamente hace lo siguiente:

1. Escoger un número entero $ q \in \mathbb{Z}^{+} $
2. Escoger un número entero positivo $ p $ que es par cuando $ q $ es impar e impar cuando $ q $ es par donde $ p < q \space \cap \space \gcd(p, q) = 1 $
3. Generar el triple primitivo $ (A, B, C) = (q^2 - p^2, 2pq, q^2 + p^2) $
4. Multiplicar por una constante $ k \in \mathbb{Z}^{+} $ para generar todos los triples derivados $ (kA, kB, kC) $

Para implementar esto en un script de Python, vamos a limitarnos a generar solo los triples primitivos (pasos 1-3) sobre un rango dado para $ p $ y $ q $. Primero, codificamos el generador:

def generar(p, q):
    A = q ** 2 - p ** 2
    B = 2 * p * q
    C = q ** 2 + p ** 2
    return A, B, C

Ahora ejecutamos dos bucles: una donde generamos todos los triples primitivos con un p par y un q impar y otra donde lo contrario es cierto. Necesitamos la biblioteca math para calcular el máximo común divisor y entonces escribiremos un bucle dentro de otro bucle que probará un rango de valores desde 1 hasta un límite superior límite:

for q in range(1, límite, 2):  # salta todos los números pares (q es impar)
    for p in range(2, q, 2):  # salta todos los números impares (p es par)
        if math.gcd(p, q) == 1:
            A, B, C = generar(p, q)
            print(A, B, C)

for q in range(2, límite, 2):  # salta todos los números impares (q es par)
    for p in range(1, q, 2):  # salta todos los números pares (p es impar)
        if math.gcd(p, q) == 1:
            A, B, C = generar(p, q)
            print(A, B, C)

En conjunto, el código es:

import math

# ¡Escriba el límite aquí!
límite = ...

def generar(p, q):
    A = q ** 2 - p ** 2
    B = 2 * p * q
    C = q ** 2 + p ** 2
    return A, B, C

for q in range(1, límite, 2):
    for p in range(2, q, 2):
        if math.gcd(p, q) == 1:
            A, B, C = generar(p, q)
            print(A, B, C)

for q in range(2, límite, 2):
    for p in range(1, q, 2):
        if math.gcd(p, q) == 1:
            A, B, C = generar(p, q)
            print(A, B, C)

Ejecutar esto con límite = 100 produce triples tan oscuros como $ (5811, 10340, 11861) $ y algunos con una diferencia de solo $ 1 $ entre dos de los números como $ (195, 19012, 19013) $. Como paso final, vamos a graficar un número finito de estos triples en el plano cartesiano con coordenadas $ (A, B) $ y una distancia $ C $ desde el origen, que se mostrará con una línea del origen hasta cada punto. Usaremos límite=20, que produce $ 78 $ triples distintos. En este momento, utilizamos matplotlib para manejar el aspecto del algoritmo que implica crear la gráfica. Entonces modificamos el código original para almacenar todos los triples en una lista en vez de mostrarlos en la pantalla inmediatamente:

import matplotlib.pyplot as plt
from matplotlib import collections as mc

límite = 20
triples = []

def generar(p, q):
    A = q ** 2 - p ** 2
    B = 2 * p * q
    C = q ** 2 + p ** 2
    return A, B, C

for q in range(1, límite, 2):
    for p in range(2, q, 2):
        if math.gcd(p, q) == 1:
            A, B, C = generar(p, q)
            triples.append((A, B, C))

for q in range(2, límite, 2):
    for p in range(1, q, 2):
        if math.gcd(p, q) == 1:
            A, B, C = generar(p, q)
            triples.append((A, B, C))

Entonces creamos una figura en matplotlib a la que podemos añadir. Definimos dos listas para almacenar las coordenadas de cada triple y entonces una tercera lista para almacenar un conjunto de líneas que convertimos en un objeto matplotlib.collections.LineCollection:

fig = plt.figure(figsize=(10, 10), dpi=200)
x = [triple[0] for triple in triples]
y = [triple[1] for triple in triples]
líneas = [[(0, 0), (x[i], y[i])] for i in range(len(x))]
figLíneas = mc.LineCollection(líneas, colors=(0.25, 0.33, 0.67, 0.25), linewidths=1)

Ahora añadimos el conjunto de líneas a un «subplot» y creamos un gráfico de dispersión que contiene los puntos. Al formatear la posición de los ejes, la parte final del código parece así:

ax = fig.add_subplot(1, 1, 1)
ax.set_title('Todos los triples pitagóricos primitivos')
ax.add_collection(figLíneas)
ax.scatter(x, y, s=5, color=(0.25, 0.33, 0.67, 1))

ax.spines.left.set_position('zero')
ax.spines.right.set_color('none')
ax.spines.bottom.set_position('zero')
ax.spines.top.set_color('none')
ax.xaxis.set_ticks_position('bottom')
ax.yaxis.set_ticks_position('left')
ax.autoscale()

plt.show()

🎊 Por fin, ¡podemos ver los resultados del algoritmo! Al ejecutar todo el programa y capturar el resultado, se produce un gráfico final verdaderamente extraordinario, mostrando una estructura interesante de los triples pitagóricos:

Graficado con el estilo SciencePlots

Aquí hay una demostración interactiva donde se puede igualar el límite a valores distintos y ver los cambios:

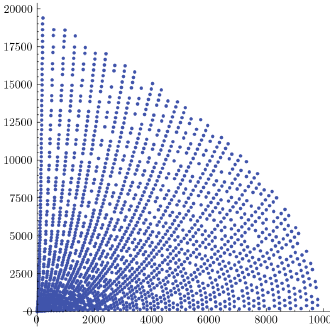
Para el gran final, aquí está el resultado de graficar los primeros $ 2000 $ triples pitagóricos primitivos (con límite=100 y sin líneas para reducir el desbarajuste):